z3-solver

简介

z3是微软最新的可满足模理论(SMT)求解器。它可以使用一个或者多个理论来检查逻辑公式的可满足性。(以下脚本不是python脚本)

z3 script

基础命令

使用echo回显信息

1	(echo "starting z3...")

声明指定类型的常量，这里声明了Int类型的a

1	(declare-const a Int)

声明函数，这里声明了一个接收整数和布尔变量并且返回整数的函数

1	(declare-fun f (Int Bool) Int)

assert可以添加公式到z3的内部栈中。假如有一个令所有声明公式都为真的解，那么我们成这些在z3栈中的公式是具有可满足性的。

(declare-const a Int)
(declare-fun f (Int Bool) Int)
(assert (> a 10))
(assert (< (f a true) 100))
(check-sat)
(get-model)

第一个声明公式表明a > 10。第二个声明公式表示函数f必须接收a和true作为传入参数，并且返回值要小于100。check-sat会说明当前在z3栈中的公式是否具有可满足性，假如具有会返回sat，否则返回unsat，有时候也会返回unknown，这说明z3不能确定公式是否是可满足的。

get-model能够获取一个解，上述脚本的返回值如下

sat
(model 
  (define-fun a () Int
    11)
  (define-fun f ((x!1 Int) (x!2 Bool)) Int
    (ite (and (= x!1 11) (= x!2 true)) 0
      0))
)

这个模型的意思是，a的值是11，对于f，传入参数有两个变量，一个是x!1为整数，另一个是x!2为布尔值。ite为if-else语句，当x!1等于11并且x!2为真时返回前一个0，否则返回后一个0。

使用视图

我们可以使用push和pop来将全局栈重点声明和断言传入当前栈中。push和pop是相匹配的。

(declare-const x Int)
(declare-const y Int)
(declare-const z Int)
(push)
(assert (= (+ x y) 10))
(assert (= (+ x (* 2 y)) 20))
(check-sat)
(pop) ; remove the two assertions
(push) 
(assert (= (+ (* 3 x) y) 10))
(assert (= (+ (* 2 x) (* 2 y)) 21))
(check-sat)
(pop)
(declare-const p Bool)
(assert p) ; error, since declaration of p was removed from the stack

返回值

1
2

sat
unsat

配置

set-option被用来配置z3。有一些选项只能在一开始被设置。我们可以使用reset命令去消除所有的声明和断言。在使用reset之后所有的配置选项都能被设置了。

(set-option :print-success true) 
(set-option :produce-unsat-cores true) ; enable generation of unsat cores
(set-option :produce-models true) ; enable model generation
(set-option :produce-proofs true) ; enable proof generation
(declare-const x Int)
(set-option :produce-proofs false) ; error, cannot change this option after a declaration or assertion
(echo "before reset")
(reset)
(set-option :produce-proofs false) ; ok

选项print-success通常在z3被另一个使用pipe的应用程序控制时特别有用。在这个模式下，那些不输出任何值的命令将打印success

其他命令

display t可以打印表达式。simplify t会打印一个可能是与t等价但是更简单的表达式。help simplify可以看到所有的可用选项。

(declare-const a (Array Int Int))
(declare-const x Int)
(declare-const y Int)
(display (+ x 2 x 1))
(simplify (+ x 2 x 1))
(simplify (* (+ x y) (+ x y)))
(simplify (* (+ x y) (+ x y)) :som true) ; put all expressions in sum-of-monomials form.
(simplify (= x (+ y 2)) :arith-lhs true)
(simplify (= (store (store a 1 2) 4 3)
             (store (store a 4 3) 1 2)))
(simplify (= (store (store a 1 2) 4 3)
             (store (store a 4 3) 1 2))
          :sort-store true)
(help simplify)

sort命令定义了一个新的排序符号，该符号是排序表达式的缩写。可以参数化新的排序符号，在这种情况下，参数的名称在命令中指定，排序表达式使用排序参数。命令的形式是这样的。（sort：the arrangement of data in a prescribed sequence）

1	(define-sort [symbol] ([symbol]+) [sort])

(define-sort Set (T) (Array T Bool))
(define-sort IList () (List Int))
(define-sort List-Set (T) (Array (List T) Bool))
(define-sort I () Int)

(declare-const s1 (Set I))
(declare-const s2 (List-Set Int))
(declare-const a I)
(declare-const l IList)

(assert (= (select s1 a) true))
(assert (= (select s2 l) false))
(check-sat)
(get-model)

运算

z3有对整数和实数的内建支持。这两种类型与机器整数（32位或64位）和浮点数不同。这两种类型(sorts)表示数学整数和实数。declare-const用于声明整型和实数常量。

(declare-const a Int)
(declare-const b Int)
(declare-const c Int)
(declare-const d Real)
(declare-const e Real)

在声明常量之后，用户可以使用断言，包含这些常数的smt公式。公式包含算术运算符。check-sat将找到一个解。该解可以通过get-model来获得。

(declare-const a Int)
(declare-const b Int)
(declare-const c Int)
(declare-const d Real)
(declare-const e Real)
(assert (> a (+ b 2)))
(assert (= a (+ (* 2 c) 10)))
(assert (<= (+ c b) 1000))
(assert (>= d e))
(check-sat)
(get-model)

实数常量需要包含一个小数点。和大多数的编程语言不同，z3不会自动的将整数转化为实数，反之亦然。to-real可以用于将整数表达式转换为实数。

(declare-const a Int)
(declare-const b Int)
(declare-const c Int)
(declare-const d Real)
(declare-const e Real)
(assert (> e (+ (to_real (+ a b)) 2.0)))
(assert (= d (+ (to_real c) 0.5)))
(assert (> a b))
(check-sat)
(get-model)

非线性运算

(declare-const a Int)
(assert (> (* a a) 3))
(check-sat)
(get-model)

(echo "Z3 does not always find solutions to non-linear problems")
(declare-const b Real)
(declare-const c Real)
(assert (= (+ (* b b b) (* b c)) 3.0))
(check-sat)

(echo "yet it can show unsatisfiabiltiy for some nontrivial nonlinear problems...")
(declare-const x Real)
(declare-const y Real)
(declare-const z Real)
(assert (= (* x x) (+ x 2.0)))
(assert (= (* x y) x))
(assert (= (* (- y 1.0) z) 1.0))
(check-sat)

(reset)
(echo "When presented only non-linear constraints over reals, Z3 uses a specialized complete solver")
(declare-const b Real)
(declare-const c Real)
(assert (= (+ (* b b b) (* b c)) 3.0))
(check-sat)
(get-model)

除法

z3也支持除法、整数除法、模和余数运算符。在内部，它们都会映射到乘法。

(declare-const a Int)
(declare-const r1 Int)
(declare-const r2 Int)
(declare-const r3 Int)
(declare-const r4 Int)
(declare-const r5 Int)
(declare-const r6 Int)
(assert (= a 10))
(assert (= r1 (div a 4))) ; integer division
(assert (= r2 (mod a 3))) ; mod
(assert (= r3 (rem a 3))) ; remainder
(assert (= r4 (div a (- 4)))) ; integer division
(assert (= r5 (mod a (- 4)))) ; mod
(assert (= r6 (rem a (- 4)))) ; remainder
(declare-const b Real)
(declare-const c Real)
(assert (>= b (/ c 3.0)))
(assert (>= c 20.0))
(check-sat)
(get-model)

在z3中，允许0作为除数，但是该运算没有特殊的结果。除法不是一个部分函数。实际上，z3中所有的函数都是总和，尽管在某些情况下，比如除0，结果可能没有被指定。rem与mod的区别在负数的时候体现。

Bitvectors

现代cpu和主流的编程语言会在固定大小的向量位上使用算术。

z3支持任意大小的位向量。

z3支持任意大小的位向量。(_ BitVec n)是长度为n的一种位向量。位向量文字可以使用二进制、十进制和十六进制表示法来定义。在二进制和十六进制情况下，位向量的大小是从字符数推断出来的。例如，二进制格式的位向量文字#b010是一个大小为3的位向量，而十六进制格式的位向量文字#x0a0是一个大小为12的位向量。对于十进制格式的位向量文字，必须指定其大小。例如，(_ bv10 32)是一个大小为32的位向量，它表示数字10。默认情况下，如果位向量大小是4的倍数，z3以十六进制格式显示位向量，否则以二进制格式显示。命令(设置选项:pp。可用于强制z3以十进制格式显示位向量字面值。

(display #b0100)
(display (_ bv20 8))
(display (_ bv20 7))
(display #x0a) 
(set-option :pp.bv-literals false)
(display #b0100)
(display (_ bv20 8))
(display (_ bv20 7))
(display #x0a)

基础Bitvector运算

(simplify (bvadd #x07 #x03)) ; addition
(simplify (bvsub #x07 #x03)) ; subtraction
(simplify (bvneg #x07)) ; unary minus
(simplify (bvmul #x07 #x03)) ; multiplication
(simplify (bvurem #x07 #x03)) ; unsigned remainder
(simplify (bvsrem #x07 #x03)) ; signed remainder
(simplify (bvsmod #x07 #x03)) ; signed modulo
(simplify (bvshl #x07 #x03)) ; shift left
(simplify (bvlshr #xf0 #x03)) ; unsigned (logical) shift right
(simplify (bvashr #xf0 #x03)) ; signed (arithmetical) shift right

Bitwise Operations(位操作)

(simplify (bvor #x6 #x3))   ; bitwise or
(simplify (bvand #x6 #x3))  ; bitwise and
(simplify (bvnot #x6)) ; bitwise not
(simplify (bvnand #x6 #x3)) ; bitwise nand
(simplify (bvnor #x6 #x3)) ; bitwise nor
(simplify (bvxnor #x6 #x3)) ; bitwise xnor

有一种快速的方法可以检验固定大小的数是否为2的幂。当且仅当x&(x-1)为0时，位向量x是2的幂或0，其中&表示位与。

Bitvectors的比较

(simplify (bvule #x0a #xf0))  ; unsigned less or equal
(simplify (bvult #x0a #xf0))  ; unsigned less than
(simplify (bvuge #x0a #xf0))  ; unsigned greater or equal
(simplify (bvugt #x0a #xf0))  ; unsigned greater than
(simplify (bvsle #x0a #xf0))  ; signed less or equal
(simplify (bvslt #x0a #xf0))  ; signed less than
(simplify (bvsge #x0a #xf0))  ; signed greater or equal
(simplify (bvsgt #x0a #xf0))  ; signed greater than

有符号比较，例如bvsle，将位向量的符号位考虑到比较中，而无符号比较将位向量视为无符号比较(将位向量视为自然数)。

Arrays

作为数学计算理论程序的一部分，McCarthy提出了阵列的基本理论，其特征是选择-存储公理。表达式select a i返回在a中i这个位置上的值，store a i v返回一个在i的位置上值为v的新array

让我们先检查数组的一个基本属性。假设a1是一个整数数组，那么约束(and (= (select a1 x) x) (= (store a1 x y) a1))是可满足的，因为当x=y时，第一个等式迫使位置x上的值为x。

(declare-const x Int)
(declare-const y Int)
(declare-const z Int)
(declare-const a1 (Array Int Int))
(declare-const a2 (Array Int Int))
(declare-const a3 (Array Int Int))
(assert (= (select a1 x) x))
(assert (= (store a1 x y) a1))
(check-sat)
(get-model)

常量数组，可以在z3中使用const构造所有位置上均为同一个值的数组。下面的示例定义了一个仅包含1的常量数组。

(declare-const all1 (Array Int Int))
(declare-const a Int)
(declare-const i Int)
(assert (= all1 ((as const (Array Int Int)) 1)))
(assert (= a (select all1 i)))
(check-sat)
(get-model)
(assert (not (= a 1)))
(check-sat)

model如下

sat
(model 
  (define-fun all1 () (Array Int Int)
    (_ as-array k!0))
  (define-fun i () Int
    0)
  (define-fun a () Int
    1)
  (define-fun k!0 ((x!1 Int)) Int
    (ite (= x!1 0) 1
      1))
)
unsat

模型提供了可满足公式中出现的自由常数和函数的解释。数组的解释与函数的解释非常相似。z3使用结构(_ as-array f)对arrays进行解释。假如数组a等于(_ as-array f)，那么对于每个索引i，(select a i)都等于(f i)。对数组常量all1进行解释。

数组上的映射函数

下面，我们将使用z3中的数组理论扩展来模拟基本的布尔代数(集合理论)。z3提供了数组上的参数化映射函数。它允许在数组范围内应用任意函数。下面的示例演示如何使用map函数。

(define-sort Set (T) (Array T Bool))
(declare-const a (Set Int))
(declare-const b (Set Int))
(declare-const c (Set Int))
(declare-const x Int)
(push)
(assert (not (= ((_ map and) a b) ((_ map not) ((_ map or) ((_ map not) b) ((_ map not) a))))))
(check-sat)
(pop)
(push) 
(assert (and (select ((_ map and) a b) x) (not (select a x))))
(check-sat)
(pop)
(push) 
(assert (and (select ((_ map or) a b) x) (not (select a x))))
(check-sat)
(get-model)
(assert (and (not (select b x))))
(check-sat)

python

示例

from z3 import *

x = Real('x')
y = Real('y')
s = Solver()
s.add(x + y > 5, x > 1, y > 1)
print(s.check())
print(s.model())

让我们从下面这个简单的例子开始

1
2
3

x = Int('x')
y = Int('y')
solve(x > 2, y < 10, x + 2*y == 7)

函数Int('x')创建了一个整型变量x。solve函数用来求解这些限制。

x = Int('x')
y = Int('y')
print(simplify(x + y + 2*x + 3))
print(simplify(x < y + x + 2))
print(simplify(And(x + 1 >= 3, x**2 + x**2 + y**2 + 2 >= 5)))

simplify用来化简公式

x = Int('x')
y = Int('y')
print(x**2 + y**2 >= 1)
set_option(html_mode=False)
print(x**2 + y**2 >= 1)

html_mode为假时将不会用html语言的形式来呈现结果，这也是默认模式。

Z3提供了遍历表达式的函数。

x = Int('x')
y = Int('y')
n = x + y >= 3
print("num args: ", n.num_args())
print("children: ", n.children())
print("1st child:", n.arg(0))
print("2nd child:", n.arg(1))
print("operator: ", n.decl())
print("op name:  ", n.decl().name())

num args:  2
children:  [x + y, 3]
1st child: x + y
2nd child: 3
operator:  &ge;
op name:   >=

Z3Py可以解非线性约束。

1
2
3

x = Real('x')
y = Real('y')
solve(x**2 + 0.12 * y**2 > 3, x**3 + y < 5)

可以使用set_option(precision=30)来决定精度

x = Real('x')
y = Real('y')
solve(x**2 + y**2 == 3, x**3 == 2)

set_option(precision=30)
print("Solving, and displaying result with 30 decimal places")
solve(x**2 + y**2 == 3, x**3 == 2)

[x = 1.2599210498?, y = -1.1885280594?]
Solving, and displaying result with 30 decimal places
[x = 1.259921049894873164767210607278?,
 y = -1.188528059421316533710369365015?]

输出中的?表示数字被截断

可以使用set_option(rational_to_decimal=True)来设置输出的格式

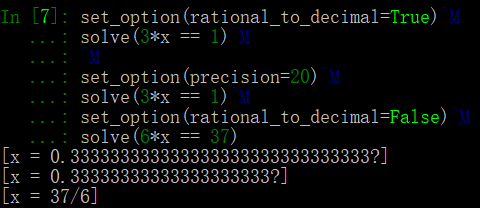
可以使用布尔逻辑运算，z3支持与(and)，或(or)，非(not)，蕴含(implies)，if(if-then-else)，与等于

a implies b 就是如果a，那么b，即if a == True, then b == True

p = Bool('p')
q = Bool('q')
r = Bool('r')
solve(Implies(p, q), r == Not(q), Or(Not(p), r))

Solvers

该类可以使用原始的z3方法，例如前文提到的check， push， pop

x = Int('x')
y = Int('y')

s = Solver()
print(s)

s.add(x > 10, y == x + 2)
print(s)
print("Solving constraints in the solver s ...")
print(s.check())

print("Create a new scope...")
s.push()
s.add(y < 11)
print(s)
print("Solving updated set of constraints...")
print(s.check())

print("Restoring state...")
s.pop()
print(s)
print("Solving restored set of constraints...")
print(s.check())

下面的例子展示了检视模型使用基本方法

x, y, z = Reals('x y z')
s = Solver()
s.add(x > 1, y > 1, x + y > 3, z - x < 10)
print(s.check())

m = s.model()
print("x = %s" % m[x])

print("traversing model...")
for d in m.decls():
    print("%s = %s" % (d.name(), m[d]))

sat
x = 3/2
traversing model...
z = 0
y = 2
x = 3/2

在上面的例子中，Reals('x y z')同时创建了变量x，y，z

m[x]返回模型m中x的值。

算术运算

z3支持实数与整数变量。他们能够在同一个问题中混用。和大多数编程语言一样，z3能够在需要的时候将整数表达式自动转成实数。下面的例子证明了声明整数和实数变量的不同方式。

x = Real('x')
y = Int('y')
a, b, c = Reals('a b c')
s, r = Ints('s r')
print(x + y + 1 + (a + s))
print(ToReal(y) + c)

ToReal方法可以将整数表达式编程实数表达式。z3Py支持所有的基础算术运算符。

例如：

a, b, c = Ints('a b c')
d, e = Reals('d e')
solve(a > b + 2,
      a == 2*c + 10,
      c + b <= 1000,
      d >= e)

simplify可以化简表达式

x, y = Reals('x y')
# Put expression in sum-of-monomials form
t = simplify((x + y)**3, som=True)
print(t)
# Use power operator
t = simplify(t, mul_to_power=True)
print(t)

化简式有两种展示风格。z3内部的选项名称用-分割各个单词。这些选项也能够在z3Py中使用。z3Py也支持Python风格的选项名称。这种风格里使用_来代替-，下面的例子展示这两种不同的风格。

x, y = Reals('x y')
# Using Z3 native option names
print(simplify(x == y + 2, ':arith-lhs', True))
# Using Z3Py option names
print(simplify(x == y + 2, arith_lhs=True))

print("\nAll available options:")
help_simplify()

大数运算

Z3Py支持大数运算。下面的例子说明了如何使用大整数、有理数、无理数进行基本算术运算。Z3Py只支持代数无理数运算。它将会用小数形式去展示无理数。内建表达可以用sexpr()方法去提取。它将会展示Lisp风格的表达式。

x, y = Reals('x y')
solve(x + 10000000000000000000000 == y, y > 20000000000000000)

print(Sqrt(2) + Sqrt(3))
print(simplify(Sqrt(2) + Sqrt(3)))
print(simplify(Sqrt(2) + Sqrt(3)).sexpr())
# The sexpr() method is available for any Z3 expression
print((x + Sqrt(y) * 2).sexpr())

[y = 20000000000000001, x = -9999979999999999999999]
2<sup>1/2</sup> + 3<sup>1/2</sup>
3.146264369941972342329135065715?
(root-obj (+ (^ x 4) (* (- 10) (^ x 2)) 1) 4)
(+ x (* (^ y (/ 1.0 2.0)) 2.0))

机器运算

现代CPU和主流编程语言使用定长比特向量来进行算术运算。机器运算在Z3Py中可以以Bit-Vetors的方式呈现。他们实现了无符号和有符号二补算术的精确语义。下面的示例演示展示了如何创建向量变量和常量。函数 BitVec('x', 16)创建了一个名字为x的16位的位向量变量。也可以创建常量，BitVecVal(10,32)创建一个大小为32的位向量，值为10

x = BitVec('x', 16)
y = BitVec('y', 16)
print(x + 2)
# Internal representation
print((x + 2).sexpr())

# -1 is equal to 65535 for 16-bit integers 
print(simplify(x + y - 1))

# Creating bit-vector constants
a = BitVecVal(-1, 16)
b = BitVecVal(65535, 16)
print(simplify(a == b))

a = BitVecVal(-1, 32)
b = BitVecVal(65535, 32)
# -1 is not equal to 65535 for 32-bit integers 
print(simplify(a == b))

x + 2
(bvadd x #x0002)
65535 + x + y
True
False

在C、C++、C#、Java中，作为数字的有符号位向量和无符号位向量之间没有区别。相反，z3提供了特殊的有符号版本的算术运算，它决定位向量是被有符号的方式处理还是被无符号的方式处理。在Z3Py中，运算符 <, <=, >, >=, /, %，>>对应于带符号的版本。对应的无符号算子是ULT、ULE、UGT、UGE、UDiv、URem、LShR

# Create to bit-vectors of size 32
x, y = BitVecs('x y', 32)

solve(x + y == 2, x > 0, y > 0)
# Bit-wise operators
# & bit-wise and
# | bit-wise or
# ~ bit-wise not
solve(x & y == ~y)

solve(x < 0)

# using unsigned version of < 
solve(ULT(x, 0))

函数

不像编程语言，有副作用（side-effects）会抛出异常或者从不返回，z3中的函数没有副作用。它们定义了所有的输入值。这包括函数，比如除法。z3基于第一顺序的逻辑。

对于约束x+y>3我们说x、y是变量。在很多教材上，x、y被称作未解释的常数。也就是这个约束允许对于任意解释x+y>3恒成立。

更准确的说，函数和在第一顺序逻辑的常量符号是未解释的或自由的，也就是说没有一个被附加的先验解释。这与属于理论签名的函数相反，比如算术，函数+有一个固定的标准解释（它是两个数字的相加）。未解释函数和常数具有最大的灵活性，它们允许任何与函数或常数上的约束一致的解释。

为了说明未解释的函数和常量，让我们使用未解释的整型常量（也就是变量）x，y，最后让f是一个未解释的函数，它接收一个类型为整型（也就是sort）的参数并得到一个整型值。这个例子说明了如何解释f对x应用一次与x不同。

x = Int('x')
y = Int('y')
f = Function('f', IntSort(), IntSort())
solve(f(f(x)) == x, f(x) == y, x != y)

[x = 0, y = 1, f = [1 -> 0, else -> 1]]

这个解读作读作f(0)=1,f(1)=0，f(a)在0和1之外都是1。

在z3中，我们也可以计算模型中约束表达式。下面的例子中演示了如何使用evaluate方法。

x = Int('x')
y = Int('y')
f = Function('f', IntSort(), IntSort())
s = Solver()
s.add(f(f(x)) == x, f(x) == y, x != y)
print(s.check())
m = s.model()
print("f(f(x)) =", m.evaluate(f(f(x))))
print("f(x)    =", m.evaluate(f(x)))
 
#In Z3, we can also evaluate expressions in the model for a system of constraints. The following example shows how to use the evaluate method.

x = Int('x')
y = Int('y')
f = Function('f', IntSort(), IntSort())
s = Solver()
s.add(f(f(x)) == x, f(x) == y, x != y)
print(s.check())
m = s.model()
print("f(f(x)) =", m.evaluate(f(f(x))))
print("f(x)    =", m.evaluate(f(x)))

可满足性和有效性

如果公式/约束F总是对未解释的符号赋值为真，则该公式/约束F是有效的。一个公式/约束F是可满足的，如果有适当的赋值给它的未解释的符号，在这个符号下F的值为真。有效性是指找到一个陈述的证据;可满足性是指找到一组约束的解决方案。考虑一个包含a和b公式F。我们可以问F是否有效,是否总是这样任意组合为a和b的值。如果F总是正确的,那么不是(F)永远是假的,然后不是(F)不会有任何令人满意的作业(例如,解决方案);也就是说，Not(F)是不能满足的。也就是说，当非(F)是不可满足的(是不可满足的)，F是有效的。或者，当且仅当非(F)是无效的(is invalid)时，F是可满足的。下面的例子证明了deMorgan定律。

下面的示例重新定义了Z3Py函数，证明它接收一个公式作为参数。此函数创建一个求解器，添加/断言公式的否定，并检查否定是否不可满足。这个函数的实现是Z3Py命令prove的一个更简单的版本。

p, q = Bools('p q')
demorgan = And(p, q) == Not(Or(Not(p), Not(q)))
print(demorgan)

def prove(f):
    s = Solver()
    s.add(Not(f))
    if s.check() == unsat:
        print("proved")
    else:
        print("failed to prove")

print("Proving demorgan...")
prove(demorgan)

List comprehension

Python支持

# Create list [1, ..., 5] 
print([ x + 1 for x in range(5) ])

# Create two lists containing 5 integer variables
X = [ Int('x%s' % i) for i in range(5) ]
Y = [ Int('y%s' % i) for i in range(5) ]
print(X)

# Create a list containing X[i]+Y[i]
X_plus_Y = [ X[i] + Y[i] for i in range(5) ]
print(X_plus_Y)

# Create a list containing X[i] > Y[i]
X_gt_Y = [ X[i] > Y[i] for i in range(5) ]
print(X_gt_Y)

print(And(X_gt_Y))

# Create a 3x3 "matrix" (list of lists) of integer variables
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(3) ]
      for i in range(3) ]
pp(X)

在上面的示例中，表达式"x%s"% i返回一个字符串，其中%s被替换为i的值。

命令pp与print类似，但是它对列表和元组使用Z3Py的格式化器，而不是Python的格式化器。

Z3Py还提供了创建布尔值、整数和实变量向量的函数。这些函数是使用列表理解实现的。

X = IntVector('x', 5)
Y = RealVector('y', 5)
P = BoolVector('p', 5)
print(X)
print(Y)
print(P)
print([ y**2 for y in Y ])
print(Sum([ y**2 for y in Y ]))

[x__0, x__1, x__2, x__3, x__4]
[y__0, y__1, y__2, y__3, y__4]
[p__0, p__1, p__2, p__3, p__4]
[y__0**2, y__1**2, y__2**2, y__3**2, y__4**2]
y__0**2 + y__1**2 + y__2**2 + y__3**2 + y__4**2

运动学方程

在高中，学生学习运动学方程。这些方程描述了位移(d)、时间(t)、加速度(a)、初速度(v_i)和末速度(v_f)之间的数学关系。用Z3Py表示，我们可以把这些方程写成:

1
2
3

a, t ,v_i, v_f = Reals('a t v__i v__f') #missing in HTML?
d == v_i * t + (a*t**2)/2,
v_f == v_i + a*t

问题1

Ima Hurryin正接近一个红绿灯，以每秒30.0米的速度行驶。灯变成黄色，Ima开始刹车并打滑停了下来。如果Ima的加速度是-8.00 m/s2，则确定汽车在打滑过程中的位移。

d, a, t, v_i, v_f = Reals('d a t v__i v__f')

equations = [
   d == v_i * t + (a*t**2)/2,
   v_f == v_i + a*t,
]
print("Kinematic equations:")
print(equations)

# Given v_i, v_f and a, find d
problem = [
    v_i == 30,
    v_f == 0,
    a   == -8
]
print("Problem:")
print(problem)

print("Solution:")
solve(equations + problem)

问题2 Ben Rushin正在等红灯。当它最终变成绿色时，本从静止开始以6.00米/s2的速度加速，持续了4.10秒。确定本的车在这段时间内的位移。

d, a, t, v_i, v_f = Reals('d a t v__i v__f')

equations = [
   d == v_i * t + (a*t**2)/2,
   v_f == v_i + a*t,
]

# Given v_i, t and a, find d
problem = [
    v_i == 0,
    t   == 4.10,
    a   == 6
]

solve(equations + problem)

# Display rationals in decimal notation
set_option(rational_to_decimal=True)

solve(equations + problem)

Bit Tricks

一些底层的hacks在C程序员中非常流行。我们在z3的实现中使用了其中的一些技巧。

二的阶乘

这个hack经常在C程序中使用（包括z3）来测试一个机器整数是否为2的幂。我们可以用z3来证明它是有效的。当且仅当x是2的幂时，x!=0&&!(x&(x-1))是正确的。

x      = BitVec('x', 32)
powers = [ 2**i for i in range(32) ]
fast   = And(x != 0, x & (x - 1) == 0)
slow   = Or([ x == p for p in powers ])
print(fast)
prove(fast == slow)

print("trying to prove buggy version...")
fast   = x & (x - 1) == 0
prove(fast == slow)

"""
And(x != 0, x & x - 1 == 0)
proved
trying to prove buggy version...
counterexample
[x = 0]
"""

相反数

下面的一个简单hack可以被用来检测两个机器整数是否是相反数。

x      = BitVec('x', 32)
y      = BitVec('y', 32)

# Claim: (x ^ y) < 0 iff x and y have opposite signs
trick  = (x ^ y) < 0

# Naive way to check if x and y have opposite signs
opposite = Or(And(x < 0, y >= 0),
              And(x >= 0, y < 0))

prove(trick == opposite)

Puzzles

狗、猫和老鼠（鸡兔同笼问题）

思考下面的智力游戏（Puzzle）。花100美元买100个动物。狗要花15美元，猫要花1美元，老鼠要花25美分。你每种至少要买一个。你需要买多少？

# Create 3 integer variables
dog, cat, mouse = Ints('dog cat mouse')
solve(dog >= 1,   # at least one dog
      cat >= 1,   # at least one cat
      mouse >= 1, # at least one mouse
      # we want to buy 100 animals
      dog + cat + mouse == 100,
      # We have 100 dollars (10000 cents):
      #   dogs cost 15 dollars (1500 cents), 
      #   cats cost 1 dollar (100 cents), and 
      #   mice cost 25 cents 
      1500 * dog + 100 * cat + 25 * mouse == 10000)

数独

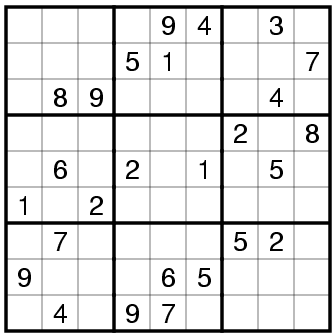
下面的例子将数度问题在z3中进行编码。不同的数独示例能够通过修改矩阵示例的方式解决。这个例子使用了很多list comprehensions。

 # 9x9 matrix of integer variables
X = [ [ Int("x_%s_%s" % (i+1, j+1)) for j in range(9) ]
      for i in range(9) ]

# each cell contains a value in {1, ..., 9}
cells_c  = [ And(1 <= X[i][j], X[i][j] <= 9)
             for i in range(9) for j in range(9) ]

# each row contains a digit at most once
rows_c   = [ Distinct(X[i]) for i in range(9) ]

# each column contains a digit at most once
cols_c   = [ Distinct([ X[i][j] for i in range(9) ])
             for j in range(9) ]

# each 3x3 square contains a digit at most once
sq_c     = [ Distinct([ X[3*i0 + i][3*j0 + j]
                        for i in range(3) for j in range(3) ])
             for i0 in range(3) for j0 in range(3) ]

sudoku_c = cells_c + rows_c + cols_c + sq_c

# sudoku instance, we use '0' for empty cells
instance = ((0,0,0,0,9,4,0,3,0),
            (0,0,0,5,1,0,0,0,7),
            (0,8,9,0,0,0,0,4,0),
            (0,0,0,0,0,0,2,0,8),
            (0,6,0,2,0,1,0,5,0),
            (1,0,2,0,0,0,0,0,0),
            (0,7,0,0,0,0,5,2,0),
            (9,0,0,0,6,5,0,0,0),
            (0,4,0,9,7,0,0,0,0))

instance_c = [ If(instance[i][j] == 0,
                  True,
                  X[i][j] == instance[i][j])
               for i in range(9) for j in range(9) ]

s = Solver()
s.add(sudoku_c + instance_c)
if s.check() == sat:
    m = s.model()
    r = [ [ m.evaluate(X[i][j]) for j in range(9) ]
          for i in range(9) ]
    print_matrix(r)
else:
    print("failed to solve")
    

# Let us remove 9 from the first row and see if there is more than one solution

instance = ((0,0,0,0,0,4,0,3,0),
            (0,0,0,5,1,0,0,0,7),
            (0,8,9,0,0,0,0,4,0),
            (0,0,0,0,0,0,2,0,8),
            (0,6,0,2,0,1,0,5,0),
            (1,0,2,0,0,0,0,0,0),
            (0,7,0,0,0,0,5,2,0),
            (9,0,0,0,6,5,0,0,0),
            (0,4,0,9,7,0,0,0,0))

instance_c = [ If(instance[i][j] == 0,
                  True,
                  X[i][j] == instance[i][j])
               for i in range(9) for j in range(9) ]    
    
def n_solutions(n):
    s = Solver()
    s.add(sudoku_c + instance_c)
    i = 0
    while s.check() == sat and i < n:
        m = s.model()
        print([[ m.evaluate(X[i][j]) for j in range(9)] for i in range(9)])
        fml = And([X[i][j] == m.evaluate(X[i][j]) for i in range(9) for j in range(9)])
        s.add(Not(fml))
        i += 1
        
n_solutions(10)

这里的If是lisp风格的写法

八皇后问题

八皇后难题是将8个国际象棋皇后放在8x8的棋盘上，这样就不会有两个皇后互相攻击。因此，解决方案要求两个皇后不能共享同一行、列或对角线。

# We know each queen must be in a different row.
# So, we represent each queen by a single integer: the column position
Queens = [ Int('Q_%i' % (i + 1)) for i in range(8) ]

# Each queen is in a column {1, ... 8 }
val_c = [ And(1 <= Queens[i], Queens[i] <= 8) for i in range(8) ]

# At most one queen per column
col_c = [ Distinct(Queens) ]

# Diagonal constraint
diag_c = [ If(i == j,
              True,
              And(Queens[i] - Queens[j] != i - j, Queens[i] - Queens[j] != j - i))
           for i in range(8) for j in range(i) ]

solve(val_c + col_c + diag_c)

应用：安装问题

安装问题包括确定是否可以在系统中安装一组新的软件包。这个应用程序时基于OPIUM：最优的包安装/卸载管理器。许多包依赖于其他包来提供一些功能。每个发行版都包含一个元数据文件，解释发行版的每个包的需求。元数据包含诸如名称、版本等细节。更重要的是，它包含了依赖和冲突条款，规定了哪些包应该安装在系统上。

使用z3可以很容易解决安装问题。它的思想是为每个包定义一个布尔变量。如果包必须在系统中，则此变量为真。如果a包依赖于b、c和z包，我们按照如下的方式写：

a, b, c, d, e, f, g, z = Bools('a b c d e f g z')

#DependsOn(a, [b, c, z])
#DependsOn is a simple Python function that creates Z3 constraints that capture the depends clause semantics.

def DependsOn(pack, deps):
    return And([ Implies(pack, dep) for dep in deps ])

#Thus, DependsOn(a, [b, c, z]) generates the constraint
# And(Implies(a, b), Implies(a, c), Implies(a, z))

print(DependsOn(a, [b, c, z]))

#That is, if users install package a, they must also install packages b, c and z.

#If package d conflicts with package e, we write Conflict(d, e). Conflict is also a simple Python function.

def Conflict(p1, p2):
    return Or(Not(p1), Not(p2))

# Conflict(d, e) generates the constraint Or(Not(d), Not(e)). 
# With these two functions, we can easily encode the example 
# in the Opium article (Section 2) in Z3Py as:

def DependsOn(pack, deps):
    return And([ Implies(pack, dep) for dep in deps ])

def Conflict(p1, p2):
    return Or(Not(p1), Not(p2))


solve(DependsOn(a, [b, c, z]),
      DependsOn(b, [d]),
      DependsOn(c, [Or(d, e), Or(f, g)]),
      Conflict(d, e),
      a, z)

def DependsOn(pack, deps):
    return And([ Implies(pack, dep) for dep in deps ])

def Conflict(p1, p2):
    return Or(Not(p1), Not(p2))

a, b, c, d, e, f, g, z = Bools('a b c d e f g z')

solve(DependsOn(a, [b, c, z]),
      DependsOn(b, [d]),
      DependsOn(c, [Or(d, e), Or(f, g)]),
      Conflict(d, e),
      a, z)

def install_check(*problem):
    s = Solver()
    s.add(*problem)
    if s.check() == sat:
        m = s.model()
        r = []
        for x in m:
            if is_true(m[x]):
                # x is a Z3 declaration
                # x() returns the Z3 expression
                # x.name() returns a string
                r.append(x())
        print(r)
    else:
        print("invalid installation profile")

print("Check 1")
install_check(DependsOn(a, [b, c, z]),
              DependsOn(b, [d]),
              DependsOn(c, [Or(d, e), Or(f, g)]),
              Conflict(d, e),
              Conflict(d, g),
              a, z)

print("Check 2")
install_check(DependsOn(a, [b, c, z]),
              #DependsOn(b, d),
              DependsOn(b, [d]),
              DependsOn(c, [Or(d, e), Or(f, g)]),
              Conflict(d, e),
              Conflict(d, g),
              a, z, g)

对于同余方程

https://www.dcode.fr/modular-equation-solver

https://github.com/55-AA/mod_equations

参考资料

https://github.com/Z3Prover/z3/wiki/Documentation

https://rise4fun.com/z3/tutorial/guide

https://github.com/Z3Prover/z3/tree/master/examples/python/tutorial/jupyter